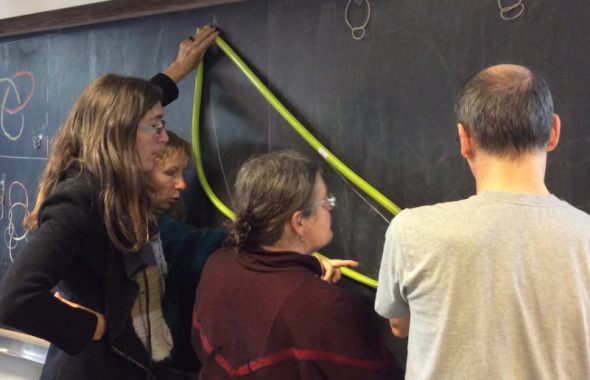C'est un fait bien connu que le plus court chemin entre deux points est la ligne droite. Et ceci est encore vrai même pour deux villes très éloignées l'une de l'autre, comme Paris et San Francisco, à condition de bien comprendre le sens de ligne droite dans ce cas. Les géomètres préférent parler de géodésique. En effet lorsqu'on regarde sur une carte plane les trajets suivis par les avions, ces derniers n'ont pas l'air de suivre des lignes bien droites... Et pourtant, les trajectoires empruntées sont bien les plus courtes possibles en distance.
Imaginons désormais deux points situés à deux altitudes différentes : on pourra penser à un skieur en haut des pistes s'apprêtant à dévaller les pentes pour rejoindre la station. Comme tout bon sprinteur, notre skieur souhaite descendre le plus rapidement possible. D'où la question assez naturelle : existe-il une forme de piste plus rapide qu'une piste qui irait en ligne droite du départ à l'arrivée ? Nous sommes d'accord que cette piste imaginaire en ligne droite serait la plus courte. Mais serait-elle pour autant la plus rapide ?
- Cette question peut être posée et étudiée à la fois en classe et en formation de professeurs.
Avec des enfants, on pourra faire un travail préparatoire, que ce soit en classe ou en cours d'éducation physique, concernant les notions de distance, de temps et de vitesse. Il est important que les enfants comprennent bien intuitivement que le plus court chemin entre deux points dans la cour est la ligne droite. Ceci s'expérimente facilement : si deux élèves s'efforcent de marcher à la même vitesse, celui qui empruntera la ligne droite arrivera avant son camarade.
- Déroulement suggéré de l'atelier :
- 15 min pour réfléchir collectivement à la question, s'assurer que tout le monde a bien compris et noter les intuitions des participants quant à l'existence d'une éventuelle autre courbe
- 10 min pour imaginer un protocole expérimental afin de tester les différentes hypothèses. On insistera sur le fait de demander un protocole réaliste !
- 40 min d'expérimentation par petits groupes de 3 à 5
- 15 min pour partager collectivement ceux qui a été observé. On pourra reproduire une manipulation devant toute la classe.
- 15 min : éclairage scientifique sur l'histoire du problème et les outils nécessaires pour le résoudre complètement.
- 15 min : les participants construisent des cycloïdes
- 10 min : synthèse collective
Voici un film de quelques minutes qui reprend l'ensemble du déroulé proposé ci-dessus. Les images ont été tournées dans une école primaire de Montargis.
Matériel proposé : des morceaux de tuyaux d'arrosage de différentes tailles. La taille de référence est choisie à 1 mètre, les autres tuyaux mesurent 1.10, 1.20, 1.30... 1.80, 1.90 et 2 mètres. Des petites billes sont également mises à disposition, ainsi que des grandes feuilles qui permettent de dessiner les trajectoires expérimentées. Enfin, dans la mesure du possible, des dispositifs d'enregistrement vidéo seront éventuellement les bienvenus pour disposer de ralentis, même si le résultat se voit sans mal à l'oeil nu.
Objectifs de la formation pour adultes :
- Vivre une mise en situation d'investigation faisant appel à des notions de mathématiques et de physique
- Envisager son réinvestissement dans les classes
Déroulé proposé pour la formation pour adultes :
- Le problème est posé : existe-t-il un chemin plus rapide que la ligne droite pour aller d'un point A à un point B ?
- Réponse écrite individuelle : 5 min
- Interaction en groupe : 10 min
- Mise en commun : 15 min
- Imaginer l'expérimentation et le matériel à utiliser pour répondre à la question (ce matériel doit pouvoir se trouver facilement...) : 10 min
- Avec le matériel, expérimenter pour avancer sur la question : 30 min
- Mise en commun : 30 min
- Éclairage scientifique autour de la chute des corps et du brachistochrone : 40 min
- Compte-rendu d'expérience : mise en œuvre d'une séance dans une classe de cycle 3 : 20 min
But des expérimentations : constater qu'il existe bien des chemins plus rapides que la ligne droite. L'intuition est qu'il est souhaitable d'avoir une trajectoire qui permette à la bille d'acquérir un maximum de vitesse dès le début.

Éclairage scientifique : il existe une et une unique courbe plus rapide que les autres. On l'appelle courbe brachistochrone, du grec brakhistos (le plus court) et chronos (le temps). On pourra lire l'article Wikipédia consacré à la courbe ; ceux que le formule mathémaitque n'effraie pas pourront lire la démonstration proposée (niveau universitaire).
Remarque importante : les expérimentations faites permettent simplement de se convaincre qu'il existe des courbes plus rapides que la ligne droite : il n'est cependant pas possible avec le matériel proposé d'en déduire que la courbe la plus rapide est unique.
En fait, cette courbe brachistochrone se construit assez facilement : c'est une cycloïde inversée. Et la cycloïde, c'est simplement la trajectoire décrite par la valve d'une roue de vélo. C'est donc très facile de construire une cycloïde avec une règle, un crayon et quelque chose de circulaire comme un pot à crayon.