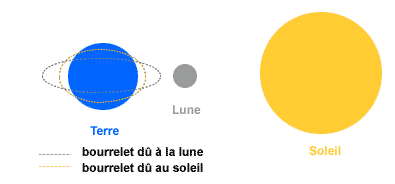
Les marées intéressent les astronomes depuis longtemps : Galilée les attribuait (à tort) à la rotation de la Terre et ce n'est que bien plus tard que Newton comprit que la clé du phénomène était dans l'attraction gravitationnelle de la Lune et (dans une moindre mesure) du Soleil.
Pourquoi des marées ?
Considérons l'influence de la Lune sur la Terre. De par sa masse, la Lune exerce une force d'attraction gravitationnelle sur notre planète. Cette force est d'autant plus importante que l'on est proche de la Lune. Le point du globe (appelons le A) situé sur l'axe Terre-Lune et du coté de la Lune est le plus attiré. Le point diamétralement opposé (notons le B) est quant-à-lui le moins attiré. Sur la figure ci-dessous, qui est une coupe équatoriale du système Terre-Lune, les flèches rouges représentent la force gravitationnelle exercée par la Lune en différents points du globe. Si cette force était partout identique (même direction et même intensité), la Terre ne subirait aucune déformation. C'est l'effet différentiel qui crée les marées. Il est représenté en vert : la force à l'origine du phénomène de marée est la différence entre la force exercée en chaque point (par exemple les flèches rouges en A, B, C et D) et la force exercée au centre de la Terre (flèche rouge centrale).
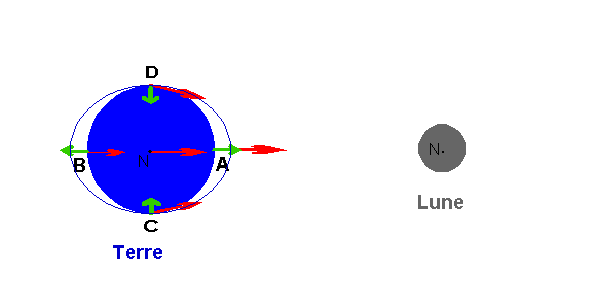
Si nous nous plaçons au centre de la Terre, que voyons nous ? D'un coté, la Terre semble attirée par la Lune (en A), et de l'autre elle semble repoussée (en B) : ceci se traduit par une déformation de notre planète qui est alors légèrement aplatie. Par rapport au centre de la Terre, les deux régions A et B sont "soulevées" en même temps. Sur la figure, la marée est haute aux points A et B et basse aux points C et D. La déformation est plus importante à l'équateur (la Lune orbite dans le plan équatorial de la Terre) et diminue graduellement vers les pôles donnant à notre planète la forme d'un ballon de rugby (l'ellipsoïde sur la figure). Notons tout de même que cette déformation est minime (de l'ordre de 40 cm à comparer avec le rayon terrestre : 6400 km) car la pesanteur est des millions de fois plus intense que la force responsable du "bourrelet". Aussi faible soit-elle, cette déformation suffit à déplacer horizontalement des masses énormes d'eau, ce qui se traduit par des amplitudes de marée pouvant atteindre 15 mètres dans la baie du Mont Saint Michel.
Notons que si la Lune ne tournait pas autour de la Terre et si la Terre ne tournait pas autour d'elle-même (à une vitesse différente), alors la Lune resterait en permanence à la verticale d'un même lieu sur Terre. Dans ce cas, la déformation serait statique, la croûte terrestre et les océans seraient dans un état d'équilibre (très) légèrement différent du cas sphérique. C'est donc l'action conjointe de la gravitation et de la rotation qui crée l'alternance des marées.
Pourquoi deux marées par jour ?
L'important ici est que la déformation induite par la Lune est symétrique et produit deux bourrelets. La révolution de la Lune autour de la Terre étant bien plus lente (27 jours) que la rotation de la Terre sur elle-même (24 heures), on peut dans un premier temps considérer la Lune comme immobile pendant que la Terre tourne. Comme l'axe des bourrelets reste l'axe Terre-Lune, un observateur fixe à la surface de la Terre va "voir passer" chacun des deux bourrelets en 24 heures, c'est-à-dire qu'il va subir deux marées par jour.
En réalité, la lente révolution de la Lune autour de la Terre fait que le cycle se décale d'environ 1/27eme de jour (un peu moins d'une heure) par jour, ce qu'on peut vérifier quotidiennement sur les horaires des marées.
L'influence de la Lune et du soleil sur les amplitudes des marées
La Lune et le Soleil sont les deux corps qui exercent une attraction gravitationnelle suffisamment importante pour provoquer les effets de marées sur la Terre. Le Soleil est bien plus massif que la Lune, mais également beaucoup plus éloigné de nous que cette dernière. Pour cette raison, le Soleil ne contribue que pour un tiers environ aux marées terrestres. Suivant les positions respectives de la Terre, de la Lune et du Soleil, les deux contributions (de la Lune et du Soleil) se renforcent, voir cas (1) plus bas, ou se neutralisent en partie, voir cas (2). Bien sûr, toutes les configurations intermédiaires sont permises...
(1) Lorsque les trois astres sont alignés, on parle de marée de vive-eau.
|
|
Les deux configurations de la Terre, la Lune et du Soleil produisant les marées de vive-eau (les échelles ne sont pas respectées) |
|
|
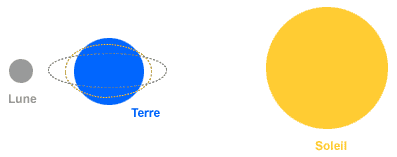
(2) Lorsque la Lune et le Soleil sont à angle droit par rapport à la Terre, on parle de marées de morte-eau
|
|
Les deux configurations de la Terre , la Lune et du Soleil produisant les marées de morte-eau (les échelles ne sont pas respectées) |
|
|
Autres conséquences importantes de l'existence des marées
La rotation de la Terre sur elle même est très rapide : par rapport à la Lune, un point de l'équateur terrestre se déplace à 1620 km/h. Le temps de réponse de la croûte terrestre est suffisamment long pour que le bourrelet soit entraîné par la rotation de la Terre : il est légèrement décalé par rapport à l'axe Terre-Lune. L'attraction gravitationnelle de la Lune sur le bourrelet exerce alors une force de rappel qui freine la rotation de la Terre et donc allonge le cycle jour/nuit. On a une preuve de ce phénomène en analysant les récifs coralliens âgés de 500 millions d'années : à l'époque, le cycle jour/nuit durait 22 heures.
Une autre conséquence, liée à la précédente est l'éloignement progressif de la Lune. La conservation de la rotation du système Terre-Lune fait que si la Terre ralentit (ce qui est le cas, voir plus haut), alors la Lune doit s'éloigner. Des mesures de la distance Terre-Lune nous montrent que notre satellite s'éloigne de nous de 4 cm par an.
Pour résumer, les marées ont comme conséquences étonnantes de rallonger la durée du cycle jour/nuit et d'éloigner la Lune de la Terre ! A terme, cet éloignement s'arrêtera lorsque la Terre tournera sur elle-même à la même vitesse que la Lune tournera autour d'elle-même et autour de la Terre : les jours seront donc aussi longs que des mois !
Pour aller plus loin
Nous avons décrit ici pourquoi nous voyons en général sur Terre deux marées par jour. Mais alors pourquoi au Vietnam, par exemple, dans le golfe du Tonkin, la ville balnéaire de Do Son ne connaît-elle qu'une seule marée par jour ? C'est évidemment parce que notre modèle est très simple : il fonctionne dans la plupart des cas, mais ne peut expliquer certaines irrégularités.
Nous avons vu plus haut deux harmoniques ou composantes de la marée : l'influence différentielle de l'attraction lunaire, et l'influence différentielle de l'attraction solaire. Mais pour être précis, il faudrait prendre en compte le fait que l'orbite de la Lune autour de la Terre ou l'orbite de la Terre autour du Soleil ne sont pas circulaires, mais elliptiques (très peu excentrées : la distance Terre-Soleil varie au maximum de 3%). Et que ces orbites ne sont pas exactement dans le même plan. Et que ces orbites évoluent avec le temps. Etc...
Il faudra également ajouter à ces composantes générales (applicables partout sur Terre) des composantes locales, dues au relief marin et côtier.
Enfin, toutes ces composantes peuvent interférer entre elles, et créer d'autres composantes. Au total, on dénombre pas moins de 143 composantes pour calculer précisément la marée en tout point du globe !!! Mais on peut localement en négliger un certain nombre (typiquement ceux qui correspondent à des marnages -amplitudes- inférieurs au millimètre) : par exemple, les marées à Brest sont calculées en utilisant "seulement" 105 des 143 composantes.
Ainsi, chacune de ces composantes a une période donnée : certaines sont semi-diurnes (elles forcent deux marées par jour), d'autres sont diurnes (elles forcent une marée par jour), d'autres mensuelles, annuelles... les produits des interactions de ces composantes peuvent quant à elle avoir des périodes quart-diurnes (4 marées par jour), voire plus complexes encore !
A Do Son, dont nous parlions plus haut, la composante qui a le plus d'influence sur la marée est une composante diurne, due à la variation de déclinaison de la Lune (sa "latitude" sur la sphère céleste) : voilà pourquoi on n'y assiste qu'à une marée par jour.
Vous pourrez trouver des explications supplémentaires sur les sites de l'IMCCE, ou de l'IFREMER.